10 - FFT¶

Lecture 10 - 08 November 2021

Brief Recap of last lecture¶

Assumption

Assume \(f(t)\) periodic with period \(NT,\ N\in\mathcal{N}^{+}_{even \neq 0}\) and \(\frac{\pi}{T}\) band limited.

The following expressions hold:

Fourier Series¶

\[\begin{align*} f(t)=\sum_{k} a_k e^{-i\omega_k t} \qquad \omega_k=\frac{2\pi}{T}k \qquad \text{Fourier Series}\\ a_k=\frac{1}{TN}\int_{-\frac{NT}{2}}^{\frac{NT}{2}} f(t) e^{i\omega_k t}dt \qquad \qquad \text{Fourier Coefficients}\\ \end{align*}\]

Coefficients¶

\[\begin{align*} F_k = \begin{cases} a_k N \quad &\text{if } 0\leq k<\frac{N}{2} \\ a_{k-N}N \quad &\text{if } \frac{N}{2}\leq k<N \\ \end{cases} \quad \iff \quad a_k = \begin{cases} \frac{F_k}{N} \quad &\text{if } 0\leq k<\frac{N}{2} \\ \frac{F_{k+N}}{N} \quad &\text{if } -\frac{N}{2}\leq k<0 \\ \end{cases} \end{align*}\]

Discrete Fourier Transform¶

\[\begin{align*} F_k = \sum_{n=0}^{N-1}f[n]e^{i \frac{2\pi}{N}nl} \end{align*}\]

Inverse Discrete Fourier Transform¶

\[\begin{align*} f[n]=\frac{1}{N}\sum_{k=0}^{N-1} F_ke^{-i\frac{2\pi}{N}kn} \end{align*}\]

Twiddle Factor¶

\[\begin{align*} W_N&=e^{i\frac{2\pi}{N}}\\ \end{align*}\]

With these expressions in mind it is possible to start developing the “Radix 2 decimation in time Fast Fourier Transfrom (FFT)”.

Fast Fourier Transform¶

Moular property of the Twiddle Factor¶

\[\begin{align*} \require{cancel} W_N^k &=e^{i\frac{2\pi}{N}} \qquad \text{write } k=k-k \text{ mod }N + k \text{ mod }N\\ &= \cancelto{1}{e^{i\frac{2\pi (k-k \text{ mod }N) N}{N}}} e^{2\pi i \frac{k \text{ mod }N}{N}} = W^{k \text{ mod }N}_N \end{align*}\]

where the fact that \(k-k \text{ mod }N\) is always an integer multiple of N (by definition) is used.

Assumption

Assume that \(N\) is a power of two, that is \(N=2^{\mu}\); \(\mu = log_2(N)\)

and separate the even and odd terms of the DFT:

\[\begin{align*} F_k = \sum_{n=0}^{N-1}f_n W^{2nk}_N &= \sum_{n=0}^{N/2-1}f_{2n}W^{2nk}_{N/2} + \sum_{n=0}^{N/2-1}f_{2n+1}W_{N/2}^{(2n+1)k} \\ &= \sum_{n=0}^{N/2-1}f_{2n}W^{nk}_{N/2} + W^{k}_{N}\sum_{n=0}^{N/2-1}f_{2n+1}W_{N/2}^{nk}\\ &= \sum_{n=0}^{N/2-1}f_{2n}W^{n(k \text{ mod }\frac{N}{2})}_{N/2} + W^k_N \sum_{n=0}^{N/2-1}f_{2n+1}W_{N/2}^{n(k \text{ mod }\frac{N}{2})} \\ &= F_{(k \text{ mod }\frac{N}{2})}^{EVEN} + W^{k}_{N}\ F_{(k \text{ mod }\frac{N}{2})}^{ODD} \end{align*}\]

This relation is, indeed, a recurrence relation. Let’s focus on it!

\[\begin{align*} W^{k}_{N} &= \begin{cases} W^{k\text{ mod } N/2}_N = W^{k}_{N} &\qquad \text{if } 0\leq k < \frac{N}{2} \\ W^{k\text{ mod } N/2+ N/2}_N &\qquad \text{if } \frac{N}{2}\leq k < N \\ \end{cases} \\ &= \begin{cases} W^{k\text{ mod } N/2}_N &\qquad \text{if } 0\leq k < \frac{N}{2} \\ -W^{k\text{ mod } N/2}_N &\qquad \text{if } \frac{N}{2}\leq k < N \\ \end{cases}\\ &= W_{N}^{k\text{ mod } N/2}\ \begin{cases} 1 &\qquad \text{if } 0\leq k < \frac{N}{2} \\ -1 &\qquad \text{if } \frac{N}{2}\leq k < N \\ \end{cases} \end{align*}\]

where the fact that \(W_{N}^{N/2}=e^{i \frac{2\pi}{N}\frac{N}{2}}=e^{i\pi}= -1\) was used. The final expression is:

\[\begin{align*} F_k &= F_{k\text{ mod }\frac{N}{2}}^{EVEN} + m(k-\frac{N}{2}) W^{k\text{ mod }\frac{N}{2}}_N F_{k\text{ mod }\frac{N}{2}}^{ODD} \\ \text{with }\quad m(l)&= \begin{cases} 1 &\text{ if } l<0 \\ -1 &\text{ if } l\geq0 \end{cases} \end{align*}\]

Example¶

The formula can be easily recalled by using the “butterfly diagram” and assuming the \(F\)s to be vectors \(F_k=\sum_{n=0}^{N-1}f_n W^{nk}_N\):

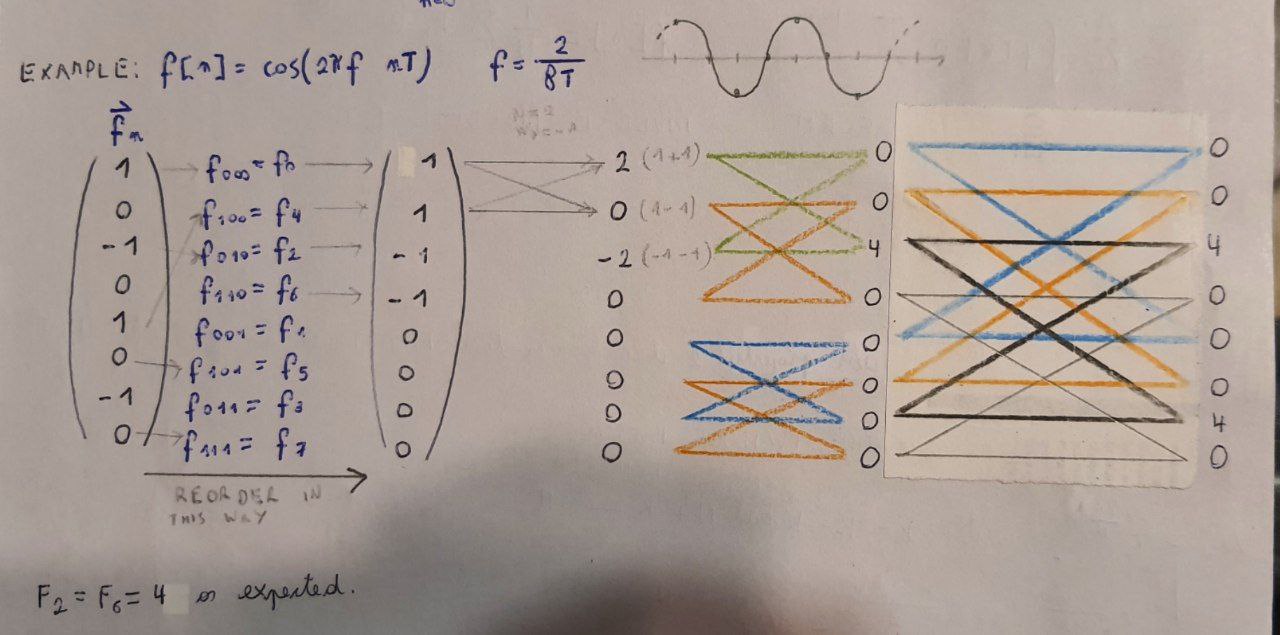
Example: Fast Fourier Transform of a cosine

As a final remark, if the number of point N is not a power of two the simplest way to perform the FFT is to pad the sequence with zeros or use windowing.

Notes of Advanced Electronics